一道基于01背包问题的经典DP题。
dp高效率的本质是memory/记忆化,因此在做dp题目时,我更倾向于找出适用的memory结构,再推导状态转移式(而不是直接找状态转移式)。下面用这题作为例子。
原题如下
给定一个数组nums,若其子数组满足所有元素的和为k,求出可能的子数组总数。(设nums中所有元素和为M)
变形一
给定一个数组nums,判断能否从该数组中不重复地取t个数,使得这t个数的和为k。(设nums中所有元素和为M)
变形二
给定一个数组nums,求出从该数组中不重复地取t个数,使得这t个数的和为k,总取法的可能数。(设nums中所有元素和为M)
变形三(代码附详细注释)
给定一个数组nums,给出任意一个具有t个元素的子数组,该子数组需满足元素和为k。(设nums中所有元素和为M)
变形四
给定一个数组nums,给出所有具有t个元素且元素和为k的子数组。(设nums中所有元素和为M)
思路与解答
破解原题的关键在于如何将这一题转化为01背包问题。整个数组的元素和为M,所以我们需要建立一个大小为M/sum的dp memory数组,对每个元素依次更新可能的情况数量。代码如下。
1
2
3
4
5
6
7
8
9
10
11
int dp_0(vector<int>& nums, int k) {
int sum = 0;
for (int& i : nums)
sum += i;
vector<int> dp(sum + 1, 0);
dp[0] = 1;
for (int i = 0; i < nums.size(); ++i)
for (int j = sum; j >= nums[i]; --j)
dp[j] += dp[j - nums[i]];
return dp[k];
}
时间复杂度O(M · n) 空间复杂度O(M)
变形一实际上是变形二的简化版,区别在于dp memory结构是二维bool还是二维int。和原题最大的不同是加入了元素个数的限制,因此这里我们的dp memory也要对应地加一维。
变形一中dp[i][j]存储的是“由j个数组成和为i的可能性”。
变形二中dp[i][j]存储的是“由j个数组成和为i的可能总数”。
代码分别如下
变形一
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
bool dp_1(vector<int>& input, int t, int k) {
cout << "Input : ";
for (int& i : input)
cout << i << ' ';
cout << endl;
cout << "t = " << t << ' ' << "k = " << k << endl;
int sum = 0;
for (int&i : input)
sum += i;
int target = sum / input.size();
vector<vector<bool>> dp(sum + 1, vector<bool>(input.size() + 1, false));
dp[0][0] = true;
for (int i = 0; i < input.size(); ++i)
for (int j = sum; j >= input[i]; --j)
for (int k = 1; k <= input.size(); ++k)
dp[j][k] = dp[j][k] | dp[j - input[i]][k - 1];
// Output DP Memory
for (int i = 0; i < dp.size(); ++i) {
cout << setw(8) << i;
for (int j = 0; j < dp[i].size(); ++j)
cout << setw(8) << dp[i][j];
cout << endl;
}
return dp[k][t];
}
变形二
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
int dp_2(vector<int>& input, int t, int k) {
cout << "Input : ";
for (int& i : input)
cout << i << ' ';
cout << endl;
cout << "t = " << t << ' ' << "k = " << k << endl;
int sum = 0;
for (int&i : input)
sum += i;
vector<vector<int>> dp(sum + 1, vector<int>(input.size() + 1, 0));
dp[0][0] = 1;
for (int i = 0; i < input.size(); ++i)
for (int j = sum; j >= input[i]; --j)
for (int k = 1; k <= input.size(); ++k)
dp[j][k] += dp[j - input[i]][k - 1];
// Output DP Memory
for (int i = 0; i < dp.size(); ++i) {
cout << setw(8) << i;
for (int j = 0; j < dp[i].size(); ++j)
cout << setw(8) << dp[i][j];
cout << endl;
}
return dp[k][t];
}
时间复杂度O(M · n^2) 空间复杂度O(M · n)
变形三在前两题的基础上增加了重建子数组的要求,但不要求计算总个数,基于这个特点我们可以对dp memory结构作如下修改,
变形一中dp[i][j]存储的是“由j个数组成和为i的可能性”,变形二中dp[i][j]存储的是“由j个数组成和为i的可能总数”,在变形三中我们需要重建序列,需要从结果一步一步反推回0。
为了构建出一条加法路径,我们需要把dp[i][j]的含义更改为“由j个数组成和为i,最后一个加入子集的数”。这样一来,通过不断地寻找最后一个数字,我们就可以完整地构建出一条路径,满足其总元素为t个,且和为k。(由于我们在遍历中是按照数组顺序将元素加入的,所以不需要考虑重复选取元素的问题)。
C++详细代码和路径复原示意图如下。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
// t个数 - 和为k - 输入数组为input
vector<int> dp_3(vector<int>& input, int t, int k) {
cout << "Input : ";
for (int& i : input)
cout << i << ' ';
cout << endl;
cout << "t = " << t << ' ' << "k = " << k << endl;
// 先求和
int sum = 0;
for (int&i : input)
sum += i;
// 构建dp memory
vector<vector<int>> dpPath(sum + 1, vector<int>(input.size() + 1, 0));
// 初态 意义为存在一条包含0个元素的路径使得元素和为0,如不加此初始条件则遍历无法进行。
dpPath[0][0] = 1;
// 第一层含义 从数组的第一个元素到最后一个元素遍历 依次加入可能的子数组
for (int i = 0; i < input.size(); ++i)
// 第二层含义 从最大可能的和开始往下遍历 依次更新dp memory
for (int j = sum; j >= input[i]; --j)
// 第三层含义 对所有可能的元素个数情况进行dp memory的更新
for (int k = 1; k <= input.size(); ++k)
// 判断条件 当这条路没有走过(!dpPath[j][k]) 且 不考虑这个元素时,存在一条包含k-1个元素的路径,其和为j减去该元素的值。
// 由于dp memory初态全为0 因此dpPath[j-input[i]][k-1]不为0即表明存在路径。
if (!dpPath[j][k] && dpPath[j - input[i]][k - 1])
// 则存在一条包含k-1+1=k个元素的路径,其和为j,将其最后一个数设为我们本次遍历的input[i]。
dpPath[j][k] = input[i];
// 输出dp memory 演示用
for (int i = 0; i < dpPath.size(); ++i) {
cout << setw(8) << i;
for (int j = 0; j < dpPath[i].size(); ++j)
cout << setw(8) << dpPath[i][j];
cout << endl;
}
// 判断是否存在可行解 如不存在直接返回
if (!dpPath[k][t]) {
cout << "Bad Input" << endl;
return vector<int>();
}
// 重建与输出
vector<int> oneResult;
// 从t个元素和为k开始往下遍历,t每次减一,k每次减掉最后一个加入的值
for (int i = t, step = k; i > 0; --i) {
oneResult.push_back(dpPath[step][i]);
step -= dpPath[step][i];
cout << oneResult.back() << ' ';
}
cout << endl;
return oneResult;
}
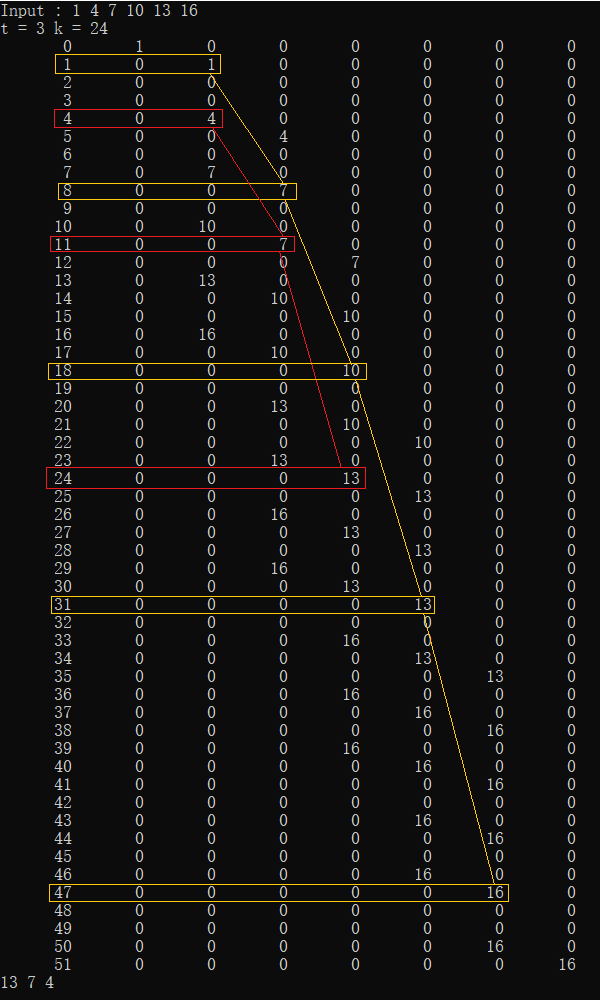
输出参考如下图
输入见第一行 红色线表示3个数和为24 结果为13-7-4 黄色线表示5个数和为47 结果为16-13-10-7-1
时间复杂度O(M · n^2) 空间复杂度O(M · n)
变形四中,需要输出全部可能的路径而非上一题的一个路径,因此我们需要再一次修改dp memory,这一次需要存储每一种可能的结果(即1-4题分别为dp memory元素分别为bool/int/int/vector),并且采用递归的写法进行重建。代码如下。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
void reconstruction4(vector<vector<vector<int>>>& data, vector<vector<int>>& result, vector<int>& input, int t, int k) {
if (!t) {
result.push_back(input);
return;
}
for (int& i : data[k][t]) {
vector<int> tmp = input;
tmp.push_back(i);
reconstruction4(data, result, tmp, t - 1, k - i);
}
}
vector<vector<int>> dp_4(vector<int>& input, int t, int k) {
cout << "Input : ";
for (int& i : input)
cout << i << ' ';
cout << endl;
cout << "t = " << t << ' ' << "k = " << k << endl;
int sum = 0;
for (int&i : input)
sum += i;
vector<vector<vector<int>>> dpPath(sum + 1, vector<vector<int>>(input.size() + 1, vector<int>()));
dpPath[0][0].push_back(1);
for (int i = 0; i < input.size(); ++i)
for (int j = sum; j >= input[i]; --j)
for (int k = 1; k <= input.size(); ++k)
if (!dpPath[j - input[i]][k - 1].empty())
dpPath[j][k].push_back(input[i]);
// Reconstruct and Output
vector<vector<int>> result;
vector<int> tmp;
reconstruction4(dpPath, result, tmp, t, k);
for (vector<int>& vec : result) {
for (int& i : vec)
cout << i << ' ';
cout << endl;
}
return result;
}
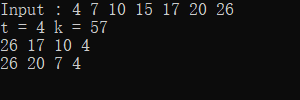
输出参考如下图
注意这样得到的结果可能会有元素的重复使用,如果需要不重复的结果,需要加哈希去重(简单做法可以直接把传值的vector换成unordered_map然后和全局计数表比较,每次加元素的时候判断,不符合则跳过)。
时间复杂度O(M · n^2)